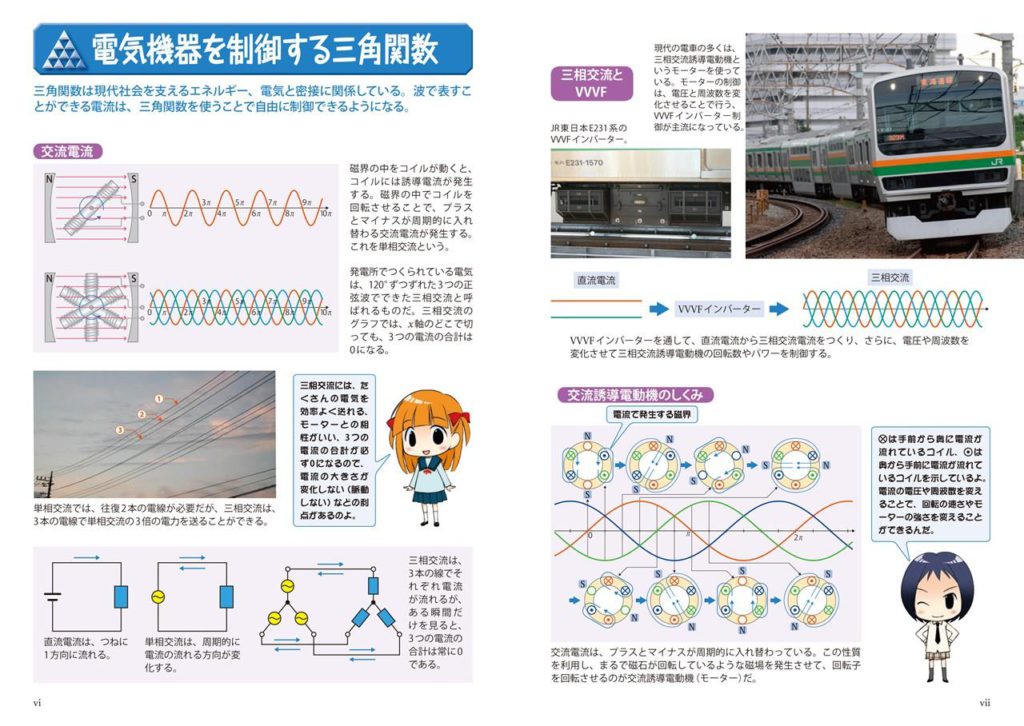
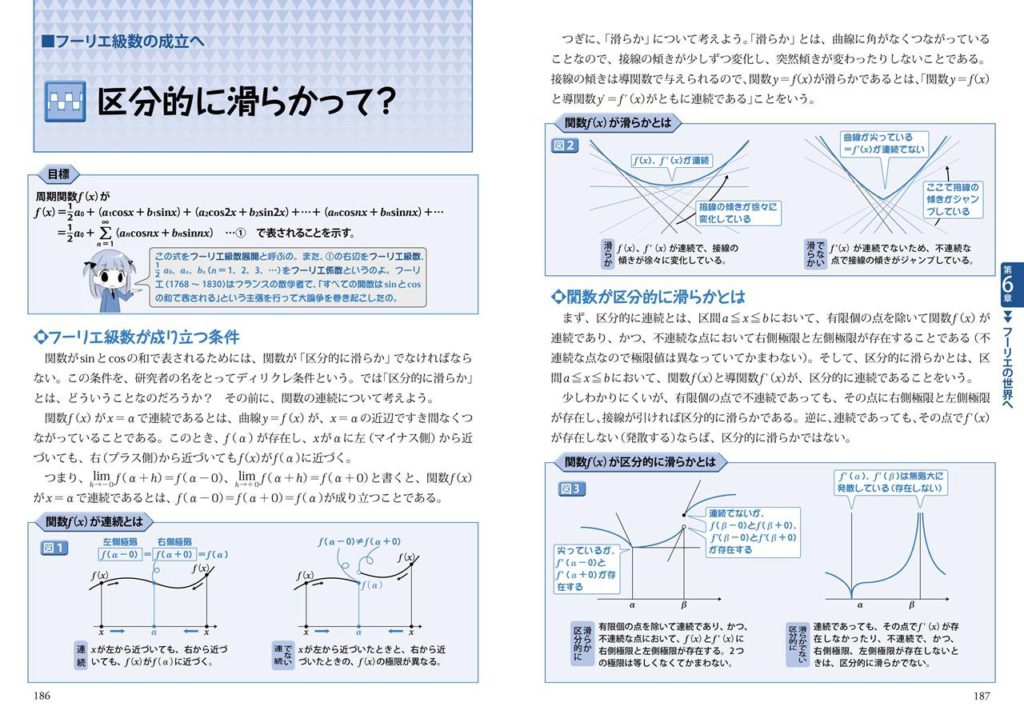
三角関数は、最も重要な数学のひとつです。大学の入試や理系企業の採用試験には、関連問題が絶対に出題されます。本書では、三角関数だけでなく、三角比、三角関数の微分積分、指数関数、フーリエ変換を、図やグラフなどで解説しています。さらに、巻頭や扉にマンガを配置して親しみやすくしました。

はじめに



第1章　三角比の誕生と性質

○三角形の相似とsin、cos、tanの登場

　三角形の相似を利用して木の高さを求めよう

　tanを使って木の高さを求めよう

　sinとcosを定義して、飛行機の高度と水平距離を調べよう

○三角比の利用

　三角比の表とその見方をおぼえよう

　噴水の高さを求めよう

　富士山の山頂で地球の半径を求めよう

○三平方の定理と無理数の計算

　自然数から実数への発展

　ピタゴラスの定理を証明しよう

　√の計算と三角比の関係を調べよう

○座標平面と三角比の拡張

　平面に番地をつけてみよう

　90°より大きな角まで三角比を拡げよう

　特別な角度の三角比を求めよう

○三角比の性質

　三角比の性質から大きな角の三角比を求めよう①

　三角比の性質から大きな角の三角比を求めよう②

　sin、cos、tanの間の関係を知ろう

　三角比から角度を求めてみよう



第2章　三角比の応用

○三角形の角と対辺の関係（正弦定理）

　湖の向こうの塔までの距離を測ってみよう

　海に浮かぶヨットまでの距離を測ってみよう

　中心角と円周角の関係を調べよう

　円形の池の直径を測ってみよう

○三角形の3辺と角の関係（余弦定理）

　見えない建物までの距離を測ってみよう

　進路を変えた飛行機の変更角度を求めよう

○正弦定理・余弦定理の利用

　正弦定理・余弦定理と三角形の合同条件

　2隻のボートの距離を求めてみよう

○図形の面積と正弦定理・余弦定理

　3辺の長さから三角形の面積を求めるヘロンの公式

　三角形の面積の公式を利用して四角形の面積を求めよう

　円に内接する四角形の面積を求めよう

　内接円・外接円の半径を求めよう

　三角錐の体積を求めよう



第3章　三角比から三角関数へ

○三角関数と弧度法

　sin、cos、tanの生い立ち

　数と数の関係を表す関数

　360°よ、さようなら！　πを使った角度の書き方

　ぐるぐる回るよ一般角

○三角関数の誕生

　三角比から三角関数への進化

　三角比の性質がそのまま三角関数の性質になる

○三角関数のグラフ

　y＝sinxとy＝cosxのグラフを描いてみよう

　正弦曲線と余弦曲線の特徴と関係を調べよう

　一風変わったy＝tanxのグラフ

　波の幅や長さを変えてみよう

　波を平行にずらしてみよう

　三角関数の変形をまとめてみよう

○三角関数の計算

　加法定理は2つの角の和の計算

　角が2倍になったらどうなるの？

　角が3倍の場合や 倍の場合

　足し算をかけ算へ　かけ算を足し算へ

　sinとcosを合わせたらどうなるの？

○媒介変数表示

　sinとcosを使って円や楕円を描こう

　sinとcosを使って曲線を描こう

○波を表す

　正弦波を詳しく見てみよう

　重ね合わせてできる波



第4章　三角関数の微分と積分

○微分を知ろう

　瞬間の速度を求めよう

　微分するってどういうこと？

○微分の計算

　xnの微分と微分の線形性

　積の微分と商の微分

　三角関数の微分

　微分してからさらに微分してみよう

○べき級数展開

　無限個のxnの和

　無限個のxnの和で関数を表す

　sinとcosを無限個のxnの和で表す

○積分とその計算

　積分は微分の逆操作

　置換積分法と部分積分法

○定積分と面積

　不定積分から定積分へ

　曲線で囲まれた図形の面積を求めよう

　定積分の置換積分法と部分積分法



第5章　三角関数と指数関数の出会い

○指数関数と対数関数

　0乗やマイナス乗ってどんな数？

　分数乗や実数乗ってどんな数？

　急激に増加する指数関数

　かけ算を足し算にする対数とは？

　ゆっくりと増加する対数関数

　exを無限個のxnの和で表そう

○iの世界への誘い

　iの世界を定義しよう

　iの世界のカケヒキ

○オイラーの公式とiの世界

　オイラーの公式を導こう

　複素数の指数法則を調べよう

　オイラーの公式からiの世界を見てみよう



第6章　フーリエの世界へ

○フーリエ級数の成立へ

　区分的に滑らかって？

　無限に伸びる関数の積分

　積分を楽にする偶関数と奇関数の性質

　フーリエ係数を求めよう

　ノコギリ波で正弦波が直線に近づく

　フーリエ余弦級数とフーリエ正弦級数

○フーリエ級数の進化

　周期2πから周期2Lの周期関数へ

　複素フーリエ級数の登場

　ノコギリ波の複素フーリエ級数を求めよう

　複素フーリエ級数を周期2Lに拡げよう

　周期関数でない関数のフーリエ級数

　方形パルスのフーリエ表現式

○フーリエ変換

　フーリエ表現式が成り立つ条件は？

　偶関数と奇関数のフーリエ変換

　フーリエ変換と微分積分の関係



第7章　フーリエの活躍

○微分方程式の基本

　微分方程式は現象の変化を表す

　微分方程式の線形性ってなに？

○微分方程式を解く

　微分方程式 ＝auを解こう

　フーリエ級数を使って微分方程式を解こう

　変数分離法で波動方程式を解こう①

　変数分離法で波動方程式を解こう②

　条件を与えて波動方程式を解いてみよう

　無限に長い棒の熱の伝わり方



　索引

　三角比の表