人気資格「電験三種」の勉強の要は「数学」といわれています。試験は計算問題が中心なので、合格するには数学の知識が不可欠です。受験者の傾向を見ると、文系の人が増えていたり、定年退職後、必要に迫られての資格取得であったりと、いわゆる“数学を苦手とする人”が多いようです。さらに理系であっても、現役から遠ざかり“自信がない人”も多いようです。そこで本書は、電験三種に合格するのに必要な数学の基礎を、初心者レベルでわかりやすく解説します

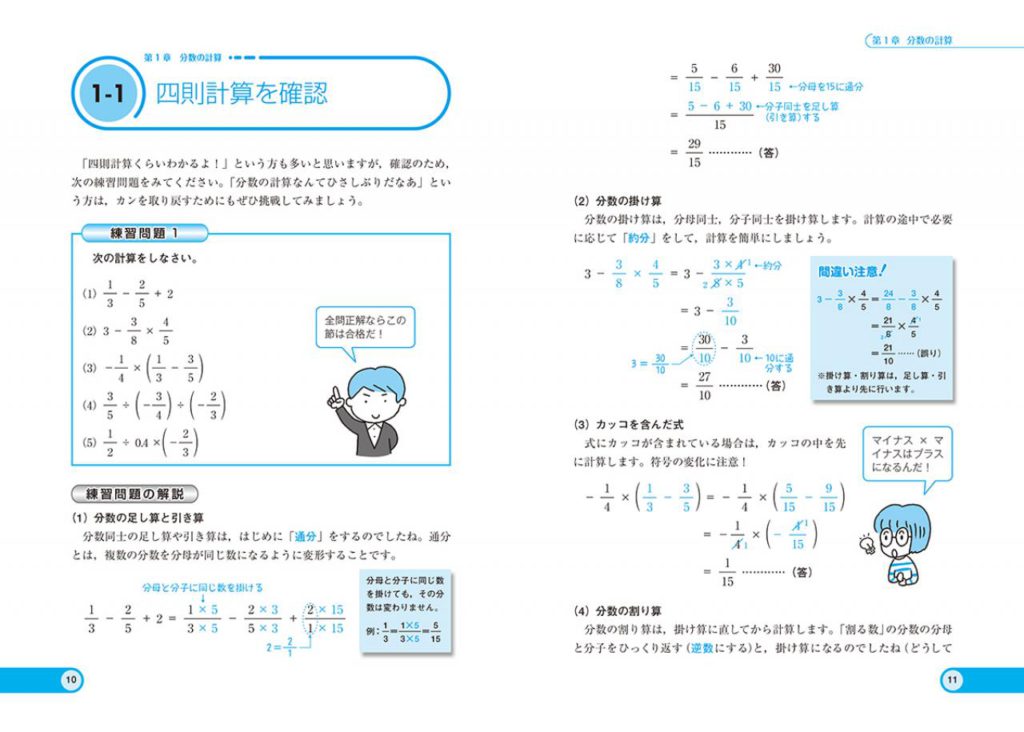
第1章　分数の計算

　1-1　四則計算を確認

　1-2　分数と小数

　1-3　分数の分数

　1-4　合成抵抗の計算

第2章　累乗とルート

　2-1　指数

　2-2　単位の換算

　2-3　平方根

　2-4　三平方の定理

　2-5　交流回路のインピーダンス

第3章　式の計算と方程式

　3-1　整式

　3-2　式の展開

　3-3　因数分解

　3-4　一次方程式

　3-5　式の変形

　3-6　連立一次方程式

　3-7　連立一次方程式の応用

　3-8　二次方程式

　3-9　二次方程式の応用

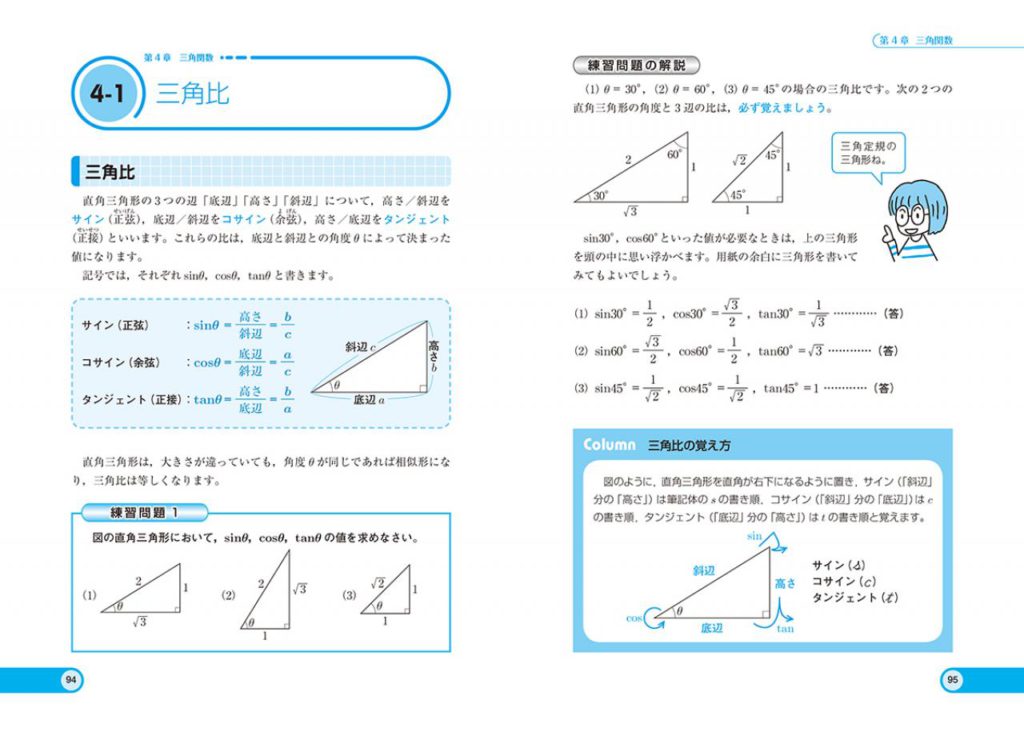
第4章　三角関数

　4-1　三角比

　4-2　三角関数の値の範囲

　4-3　余弦定理と加法定理

　4-4　弧度法（ラジアン）

　4-5　三角関数と交流

第5章　ベクトル

　5-1　ベクトルとは

　5-2　ベクトルの成分表示

　5-3　ベクトルの極座標表示

　5-4　交流とベクトル

　5-5　ベクトルの内積と力率

第6章　複素数

　6-1　複素数とは

　6-2　複素数とベクトル

　6-3　複素数によるベクトル演算

　6-4　複素数と交流

　6-5　三相交流の原理

　6-6　三相交流回路の計算

第7章　もっと知りたい電気数学

　7-1　最小定理とその応用

　7-2　三相交流の電力測定

　7-3　対数と利得

　7-4　過渡現象について

　7-5　ラプラス変換

　7-6　論理演算