フーリエ変換とは、フーリエが考えた数学でできた道具のことです。

私たちの生活に必要なディスプレイ表示やデータ通信では、フーリエ変換が欠かせません。

本書では、重要なポイントを押さえながら、数式をひとつひとつを掲載して解説しました。

理系の大学生や技術者が理解しておかなくてはならないフーリエ変換を、本書でマスターしてください。

はじめに



Chapter 1　フーリエ級数前夜

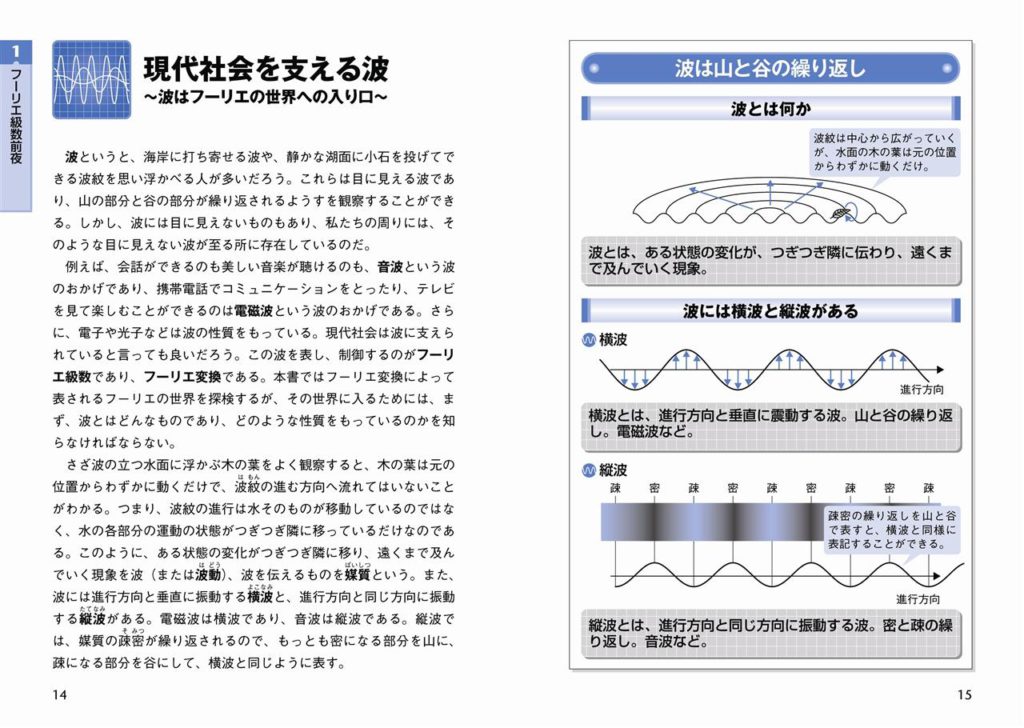
現代社会を支える波　波はフーリエの世界への入り口

重ね合わせの原理　複雑な波の性質を知るために整った波を調べる

正弦、余弦、正接　円とラジアン単位で三角比を定義する

正弦波を表す関数　単位円を使ってサインカーブを描く

正弦波の特徴　周期と振幅を変えた関数のグラフ

波の移動　平行移動した関数のグラフ

波の特徴　位置の関数と時間の関数で表す

偶関数と奇関数　y軸に関して対象な関数と原点に関して対象な関数

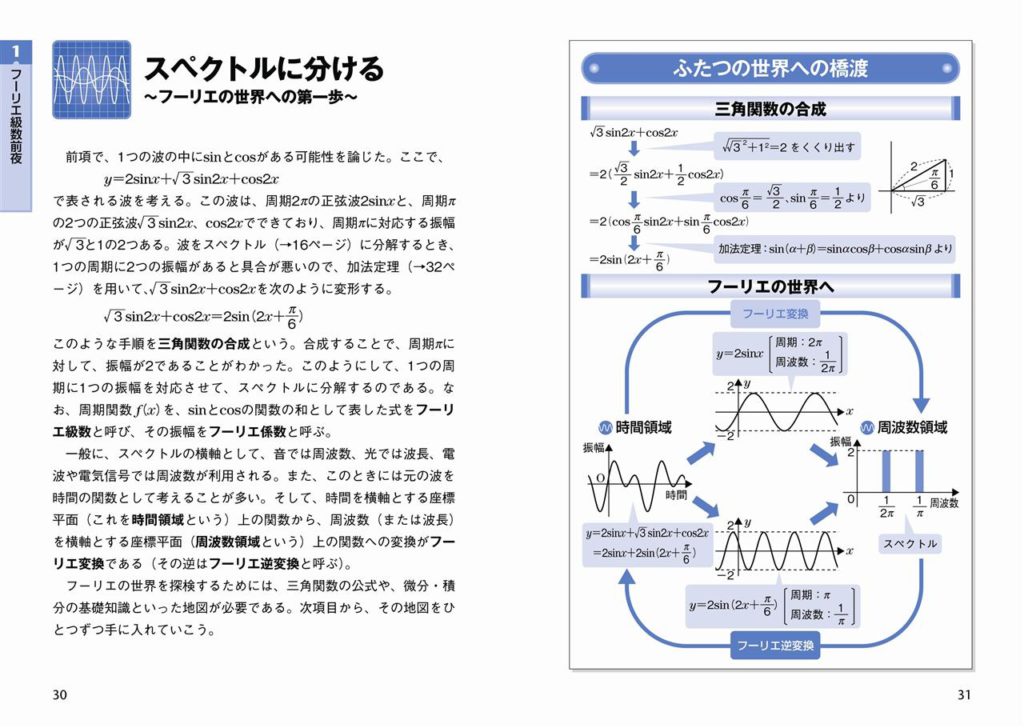
スペクトルに分ける　フーリエの世界への第一歩

三角関数の公式①　もっとも基本となる公式

三角関数の公式②　加法定理から導かれる公式

三角関数のかけ算　かけ算を足し算に変える

微分積分の準備　微分係数は曲線の接線の傾き

微分とは何か？　導関数を求めることが微分の基本

三角関数の微分　sinxはcosxへ、cosxは-sinxへ

べき級数展開　sinxを無限個のx^nの和にする

積分とは何か？　微分を逆の操作したものが積分

リーマン和　細長い長方形から面積を求める

定積分と面積　微分の定義を使った証明

曲線に挟まれた面積　定積分に＋－をつけて計算

置換積分と部分積分　積分の計算テクニック

広義積分　無限に伸びる関数の積分

コラム　フーリエ級数とディリクレ条件



Chapter 2　フーリエ級数の世界

関数の滑らかさ　区分的に滑らかであるとは？

フーリエ級数をめざして①　フーリエ係数を求める(1)

フーリエ級数をめざして②　フーリエ係数を求める(2)

ノコギリ波のフーリエ係数　正弦波が直線に近づく

不連続点ではどうなるのか？　右側極限と左側極限の平均で示される

フーリエ級数に到達　フーリエ余弦級数展開とフーリエ正弦級数展開

「関数に近づく」とは　各点収束と一様収束

フーリエ級数を微分する　関数の微分と項別微分

フーリエ級数を積分する　関数の積分と項別積分

ノコギリ波を項別微分可能にする　超関数の世界へ

デルタ関数のフーリエ級数　フーリエ級数が無限大もカバー

デルタ関数の性質　デルタ関数は関数f(x)の値を取り出す

デルタ関数の相棒　単位階段関数

ノコギリ波の微分①　ノコギリ波を単位階段関数で表す

ノコギリ波の微分②　超関数としての微分と項別微分

周期2Lのフーリエ級数　周期2πから周期2Lへ

フーリエ級数とベクトル　ベクトルとは方向と大きさをもった量

ベクトル空間　基底となるベクトルの個数が次元を表す

フーリエ級数のつくる世界　無限次元ベクトル空間

フーリエ級数の近づきかた　平均収束とは

パーシヴァルの等式　フーリエの世界は完全正規直交関数系



Chapter 3　複素フーリエ級数

複素フーリエ級数　フーリエ級数を進化させる新たなステージ

指数の拡張　指数を自然数から実数へ拡げる

対数の導入　かけ算を足し算で計算する工夫

指数関数と対数関数　表裏一体の指数と対数の関係

指数関数と対数関数の微分　微分しても変わらない関数と分数に変わる関数

指数関数と対数関数のべき級数展開　e^x、log(1+x)を展開する

2つの実数とiからなる数　実数の外に広がる複素数の世界

複素数の性質　複素数で四則演算を行おう

iの世界の指数関数　指数関数を拡張する

オイラーの公式　三角関数と指数関数の出会い

複素フーリエ級数　cnとc-nは表と裏の関係

複素フーリエ級数の性質と拡張　周期2Lの関数の複素フーリエ級数



Chapter 4　フーリエ変換

非周期関数のフーリエ表現式①　周期関数から非周期関数へ

非周期関数のフーリエ表現式②　方形パルスのフーリエ表現式

フーリエの積分定理　フーリエ表現式が成り立つための条件

フーリエ変換とフーリエ逆変換　フーリエ変換の定義は2通りある

スペクトル　フーリエ変換が表すものの意味

フーリエ余弦変換とフーリエ正弦変換　偶関数のフーリエ変換・奇関数のフーリエ変換

フーリエ変換の性質①　f(x)とF(ω)の関係

フーリエ変換の性質②　フーリエ変換と微分・積分

指数関数のフーリエ変換　ローレンツ型関数の出現

ガウシアンのフーリエ変換　ガウシアンからガウシアンへの変換

デルタ関数のフーリエ変換　デルタ関数は1になる

デルタ関数を用いたフーリエ変換　超関数としてのフーリエ変換

合成積　合成積の意味とそのフーリエ変換

エネルギースペクトル　フーリエ変換のパーシヴァルの等式



Chapter 5　フーリエ変換の活躍

微分方程式　現象の関係を表す数式

線形微分方程式　解の重ね合わせと線形性

双曲線関数　三角関数によく似た性質の関数

波動方程式①　変数分離法で波動方程式を解く

波動方程式②　境界条件で解を絞り込む

波動方程式③　初期条件にあわせる

波動方程式④　弦の振動を式で表そう

熱伝導方程式①　両端が断熱の物体の熱伝導(1)

熱伝導方程式②　両端が断熱の物体の熱伝導(2)

熱伝導方程式③　無限に長い棒状の物体の熱伝導(1)

熱伝導方程式④　無限に長い棒状の物体の熱伝導(2)

ラプラスの方程式①　定常状態の方程式(1)

ラプラスの方程式②　定常状態の方程式(2)

ラプラスの方程式③　静電気のポテンシャル場



Chapter 6　離散フーリエ変換

サンプリング　アナログからデジタルへ

サンプリング定理①　ナイキスト間隔とサンプリング間隔

サンプリング定理②　サンプリング関数で表す

離散フーリエ変換①　サンプル値をフーリエ変換する

離散フーリエ変換②　離散フーリエ逆変換を導く

行列の導入　数をまとめて計算するために

フーリエ行列①　離散フーリエ変換の行列表示

フーリエ行列②　離散フーリエ変換の具体例

離散フーリエ変換の性質　離散フーリエ変換と振幅

離散フーリエ変換の利用　ノイズを取り除く

高速フーリエ変換　計算回数を減らしてスピードアップ



Chapter7　ラプラス変換

ヘビサイドとラプラス変換　微分方程式と代数方程式の橋渡し

指数位数の関数　ラプラス変換が可能であるための条件

基本的な関数のラプラス変換　n次関数・指数関数・三角関数のラプラス変換

ラプラス変換の性質①　性質を使って計算を容易にする

ラプラス変換の性質②　微分・積分とラプラス変換の関係

ラプラス逆変換　代表を選んで対応させる

基本的な関数のラプラス逆変換　使いやすく書き換える

ラプラス変換の応用①　減数振動の方程式

ラプラス変換の応用②　減衰振動の3つのパターン

ラプラス変換の応用③　a^2-b^2が0または負の場合